unidad 5
5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales.Una recta tangente a una curva en un punto, es una recta que al pasar por dicho punto y que en dicho punto tiene la misma pendiente de la curva. La recta tangente es un caso particular de espacio tangente a una variedad diferenciable de dimensión.
Sea
una curva, y 
un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en la curva no cambia repentinamente de dirección. La tangente a en es la recta 
que pasa por y que tiene la misma dirección que alrededor de .La tangente es la posición límite de la recta secante (
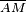) (el segmento 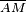se llama cuerda de la curva), cuando 
es un punto de que se aproxima indefinidamente al punto ( se desplaza sucesivamente por 
Si
representa una función f (no es el caso en el gráfico precedente), entonces la recta 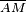tendrá como coeficiente director (o pendiente):
Donde
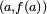son las coordenadas del punto y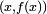 
las del punto . Por lo tanto, la pendiente de la tangente TAserá:
Es, por definición, f '(a), la derivada de f en a.
La ecuación de la tangente es
:
La recta ortogonal a la tangente
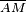que pasa por el punto 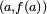se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por 
. Siendo su ecuación:
suponiendo claro está que
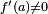. Si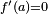 
entonces la recta normal es simplemente 
. Esta recta no interviene en el.
No hay comentarios:
Publicar un comentario