4.5 Regla de la cadena
En cálculo, la regla de la cadena es una fórmula para la derivada de la composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas cuando existecomposición de funciones
Demostración de la regla de la cadena
Sea
Esto es entonces
Aplicando la definición de derivada se tiene
Donde queda
Equivalentemente, multiplicando y dividiendo entre 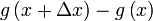 (esta demostración solo vale cuando
(esta demostración solo vale cuando 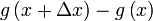 es distinto de cero , por ejemplo si g(x) fuera constante no se cumple)
es distinto de cero , por ejemplo si g(x) fuera constante no se cumple)
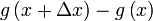 (esta demostración solo vale cuando
(esta demostración solo vale cuando 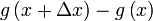 es distinto de cero , por ejemplo si g(x) fuera constante no se cumple)
es distinto de cero , por ejemplo si g(x) fuera constante no se cumple)

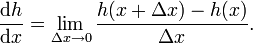


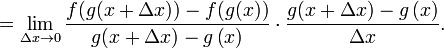

No hay comentarios:
Publicar un comentario