4.3 concepto de diferencial ,interpretación geométrica de las diferenciales.
Existen muchas situaciones, dentro y fuera de las matemáticas, en que necesitamos estimar una diferencia, como por ejemplo en las aproximaciones de valores de funciones, en el cálculo de errores al efectuar mediciones (Valor real menos valor aproximado) o simplemente al calcular variaciones de la variable dependiente cuando la variable independiente varía "un poco", etc. Utilizando a la recta tangente como la mejor aproximación lineal a la función en las cercanías del punto de tangencia, aproximaremos esta DIFERENCIA con la diferencia sobre la recta tangente, a la que llamaremos EL DIFERENCIAL de la función en el punto.
DEFINICIÓN Y EJEMPLOS
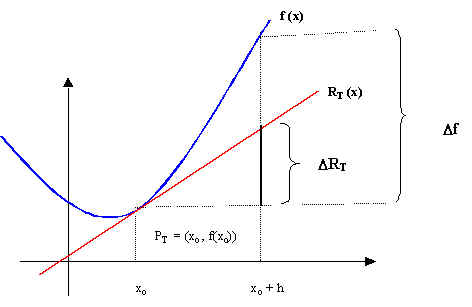
Consideremos la siguiente ilustración en donde aproximamos a la función f por su recta tangente.
Interpretación geométrica
Geometricamente, ¿qué es la derivada de
en un punto 
?La diferencia
mide el incremento de la función entre y 
, mientras que 
mide el incremento de la variable. El cociente entre ambos incrementos 
es precisamente la pendiente de la recta secante a la gráfica de la función, entre los puntos 
y 
. En la siguiente gráfica podemos observar que ocurre cuando tomamos valores de la variable cada vez más proximos al punto 
El límite de las secantes conforme
tiende a es la recta tangente a la gráfica en el punto . Así pues el límite de las pendientes de las secantes es la pendiente de la tangente, y por tanto podemos interpretar 
como la pendiente de la recta tangente en el punto .http://www.matap.uma.es/~garvin/05Ca04/node4.html
No hay comentarios:
Publicar un comentario